Odds Of Getting 4 Of A Kind In Texas Holdem easily progress to making smart blackjack bets quickly. Practice using one of our 50 free blackjack games now before playing blackjack for Odds Of Getting 4 Of A Kind In Texas Holdem real money.
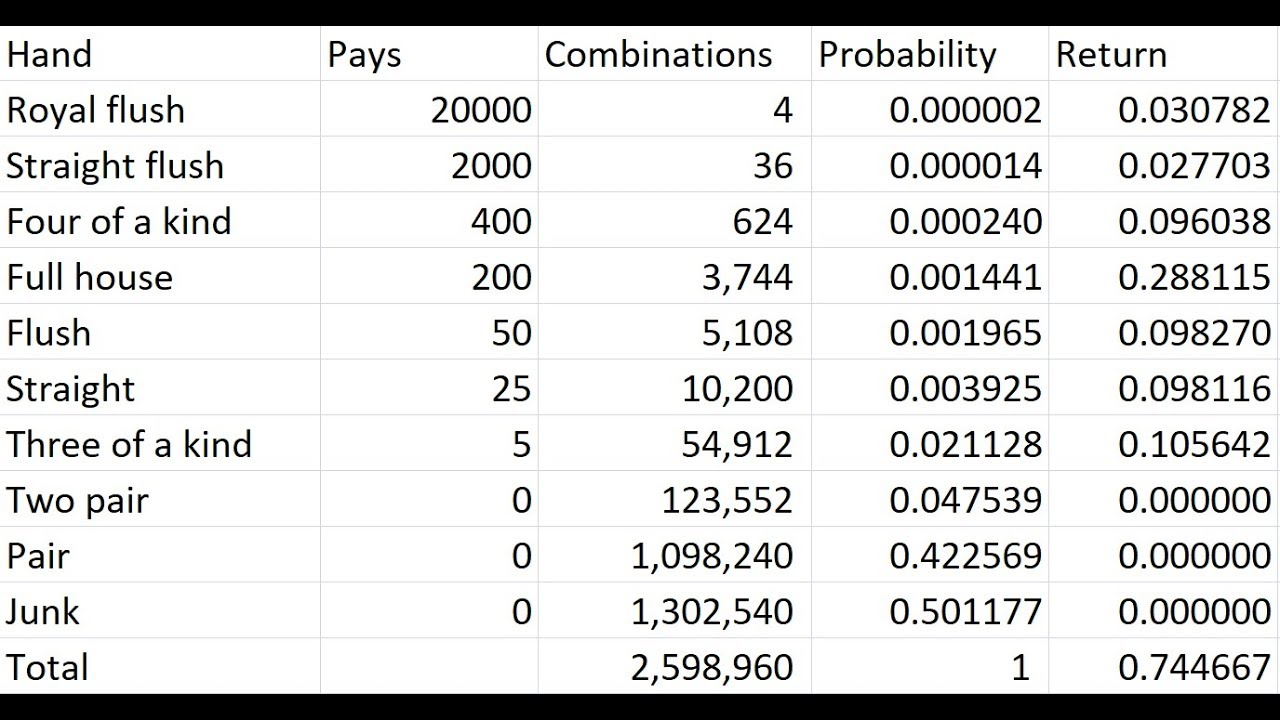
Question: What is the probability of a 4 of a kind appearing on the board in texas holdem?
- Odds Of 4 Of A Kind Texas Holdem Berryburst Max are subject to change & must be used within 3 days from activation. Bonus spins are activated after wagering a min. The welcome bonus Odds Of 4 Of A Kind Texas Holdem and spins must be wagered 35x times before the bonus or any winnings can be withdrawn. Stake using bonus is £5.
- This makes the probability of drawing to a full house or four of a kind on the turn or river 0.334 and the odds are 1.99: 1. This makes drawing to a full house or four of a kind by the river about 8½ outs.
- Probability Of Getting 4 Of A Kind In Texas Holdem While our vetting process is very in-depth, the following summarized Probability Of Getting 4 Of A Kind In Texas Holdem elements make up the foundation of what we – and you! – should always insist upon in a Probability Of Getting 4 Of A Kind In Texas Holdem reputable USA online casino site.
Solution:
- All of the following computations assume that you know only your two hole cards, and no other cards are known to you. Thus, there are 50 unknown cards after you see your hole cards.
- In the computations below, I'll use the symbol X for the card that does not fill the 4 of a kind, and an M for the cards that do fill the 4 of a kind.
- If you do not hold a pair, the probability is different than if you do hold a pair. So, we need to analyze these two cases seperately. The probability (denoted P) of getting a paired hand in the hole is 3/51=.0588235 (your first card from the deck can be any card, while the second must match it; after you get your first hole card, there are 3 cards of the 51 remaining cards that match your hole card). Thus, the probability of getting a non-paired hand is 1-.0588235=.94117647.
Case 1. Let's analyze non-paired hole cards first.
- Scenario 1: XMMMM
- Start with non-paired hole cards P=.94117647.
- X can be any card (even one that pairs either of your hole cards), and there are 50 cards remaining in the deck, so it has P=50/50.
- The first M, M1, can be any card not matching X (there are 3 that do match X) nor either of your hole cards (because if it did, no 4 of a kind on the board is possible; there are 6), and there are 49 cards remaining in the deck, so it has P=40/49.
- The second M, M2, must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48
- The third M, M3, must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47
- The fourth M, M4, must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now multiplying .94117647*(50/50)*(40/49)*(3/48)*(2/47)*(1/46) gives us the probability that there will be a 4 of a kind on the board in the form XMMMM, or P=.00004442.
- Scenario 2: MXMMM
- Start with non-paired hole cards P=.94117647.
- M1 can be any card not matching either of your hole cards (there are 6), and there are 50 cards remaining in the deck, so it has probability P=44/50.
- X can be any card not matching M1 (there are 3), and there are 49 cards remaining in the deck, so it has P=46/49.
- M2 must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48.
- M3 must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47.
- M4 must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now, multiplying gives us the probability that there will be a 4 of a kind on the board in the form MXMMM, or P=.00004495.
- Scenario 3: MMXMM
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(X) = 46/48 (must not match M1; there are only 2 cards left that do match M1)
- P(M3) = 2/47 (must match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMXMM is P=.00004495.
- Scenario 4: MMMXM
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(X) = 46/47 (must not match M1; there is only 1 card left that does match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMMXM is P=.00004495.
- Scenario 5: MMMMX
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(M4) = 1/47 (must match M1)
- P(X) = 46/46 (must not match M1; there are 0 cards left that match M1 since they are all on the board)
- Probability that there will be a 4 of a kind on the board in the form MMMMX is P=.00004495.
Adding all 5 of these probabilities gives us a total probability that there will be any 4 of a kind on the board when holding a non-pair in the hole, or P=.0002297.
Case 2. Analyze paired hole cards.
- Scenario 1: XMMMM
- Start with paired hole cards P=.05882353.
- X can be any card (even one that pairs either of your hole cards), and there are 50 cards remaining in the deck, so it has P=50/50.
- The first M, M1, can be any card not matching X (there are 3) nor either of your hole cards (because if it did, no 4 of a kind on the board is possible; there are 2), and there are 49 cards remaining in the deck, so it has P=44/49.
- The second M, M2, must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48
- The third M, M3, must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47
- The fourth M, M4, must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now multiplying .05882353*(50/50)*(44/49)*(3/48)*(2/47)*(1/46) gives us the probability that there will be a 4 of a kind on the board in the form XMMMM, or P=.00000305.
- Scenario 2: MXMMM
- Start with paired hole cards P=.05882353.
- M1 can be any card not matching either of your hole cards (there are 2), and there are 50 cards remaining in the deck, so it has probability P=48/50.
- X can be any card not matching M1 (there are 3), and there are 49 cards remaining in the deck, so it has P=46/49.
- M2 must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48.
- M3 must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47.
- M4 must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now, multiplying gives us the probability that there will be a 4 of a kind on the board in the form MXMMM, or P=.00000307.
- Scenario 3: MMXMM
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(X) = 46/48 (must not match M1; there are only 2 cards left that do match M1)
- P(M3) = 2/47 (must match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMXMM is P=.00000307.
- Scenario 4: MMMXM
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(X) = 46/47 (must not match M1; there is only 1 card left that does match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMMXM is P=.00000307.
- Scenario 5: MMMMX
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(M4) = 1/47 (must match M1)
- P(X) = 46/46 (must not match M1; there are 0 cards left that match M1 since they are all on the board)
- Probability that there will be a 4 of a kind on the board in the form MMMMX is P=.00000307.
Adding all 5 of these probabilities gives us a total probability that there will be any 4 of a kind on the board when holding a pair in the hole, or P=.00001513.
So, now we add the two probabilities together to get the total probability of a 4 of a kind appearing on the board regardless of if your hole cards are paired or not: .0002297+.00001513=.00023955, or 4174.46 to 1.
To put this in perspective, if you played 5 days a week, 8 hours a day in a live card room at 25 hands per hour, you would see 1000 hands a week. Furthermore, IF every hand went to the river OR if you rabbit-hunted every hand and looked at all the board cards regardless of if play dictated that they be shown, you'd see a 4 of a kind on the board once a month or so. Of course, since only approximately 20% of all hands go to the river, a full-time live card room player will only see about 2 or 3 a year.
Online players generally see twice as many hands as a player in a live card room; they will see twice as many 4 of a kinds on the board than will a player that plays the same amount of time in a live poker room.
Online Play: There are manyonline sites where you can play this style of poker -- but you need to make sure that the site accepts players fom your area of residence.

- US players should use the links below to find a poker room
- All sites that accept players from your area
- All sites that accept players from your area and that offer a free, no-deposit bonus to try the games risk-free
- All sites that accept players from your area and that offer at least a 50% initial deposit bonus should you decide to make a deposit
- Players outside of the United States have additional choices, and should use the links below to find a poker room
- All sites that accept players from your area
- All sites that accept players from your area and that offer a free, no-deposit bonus to try the games risk-free
- All sites that accept players from your area and that offer at least a 50% initial deposit bonus should you decide to make a deposit
Recommended Sites: These sites have nice bonuses, great game selection, and excellent sit-and-go tournaments at all stakes. All take players from the US (as well as most non-US players, of course), and have at least a 100% initial deposit bonus for new players.
- Bovada Poker: 110% bonus!
- Americas Cardroom: 100% bonus!
- OddsMaker.com Poker: 100% bonus!
Odds Of 4 Of A Kind In Texas Hold'em
Freerolls: You can play this game for free with the chance to win real cash. Check out the online poker freeroll listings to find the date, time, and location of an upcoming freeroll.
Odds Of Getting 4 Of A Kind In Texas Hold Em
For more information...
Good luck and have fun!